The link between two candidates marked 8, highlighted in yellow and orange in row E, is strong. If one of those candidates is removed, the other candidate 8 should be a valid solution since there is no other candidate 8 in row E. This statement does not hold true for the two candidates marked 8, highlighted in yellow and orange in row C. If one of the candidates in row C is removed, the other candidate 8 is not necessarily a valid solution since there are other candidates 8 in row C. The link between candidates 8 in row C is weak. For weak links, we can only say that if one candidate is a valid solution, the linked candidate should be removed, since only one candidate 8 is allowed in each row, column, and square. This statement is valid for both strong and weak links.

The difference between the Simple Coloring technique and the X-Chain is that in Simple Coloring, all links are strong, while in the X-Chain, strong links alternate with weak links. It is not necessary for the beginning and end candidates of the X-Chain to be linked, but the X-Chain should start and end with strong links. Usually, linked X-Chain candidates are colored alternately with two colors. The most important property of the X-Chain is that if one candidate in the chain is a valid solution, then all candidates with the same color are valid solutions, and all candidates with the other color can be removed, and vice versa.

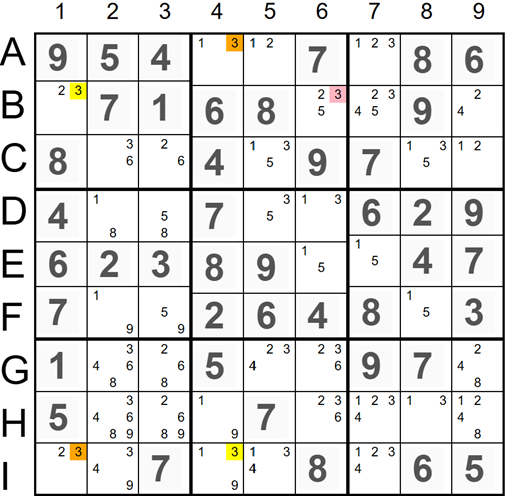
Candidate '3' marked in red in cell B6 can 'see' (is in the same row as) the yellow candidate '3' in cell B1 and (in the same 3x3 square as) the orange candidate '3' in cell A4. The X-Chain is formed by four candidates marked '3' in cells A4, I4, I1, and B1. There is a strong link between candidates '3' in cells A4 and I4, a weak link between candidates '3' in cells I4 and I1, and a strong link between candidates '3' in cells I1 and B1.

If the orange candidate '3' in cell A4 is not a solution, then the yellow candidate '3' in cell I4 should be a solution since there is a strong link between them. Then, '3' in I3 should be removed as there is a weak link, and candidate '3' should be a solution. In this case, all yellow candidates in the X-Chain are the solution, and all orange candidates should be removed. Conversely, if the yellow candidate '3' in cell B1 is not a solution, the orange candidate '3' in I1 should be a solution, yellow '3' in cell I4 should be removed, and the orange candidate '3' should be removed. In this case, all yellow candidates in the X-Chain should be removed, and all orange candidates are the solution.

Since the 'off-chain' candidate '3' marked in red in cell B6 can 'see' both yellow and orange candidates, and one of them is definitely a solution, this candidate should be removed.

The image on the left shows another example of the X-Chain - Two Colours 'Elsewhere' technique. The X-Chain consists of three yellow candidates marked '8' and three orange candidates. The 'off-chain' candidate '8' marked in red in cell A7 is in the same row A as the yellow candidate '8' in cell A2 and in the same column as the orange candidate '8' marked in cell E7. Therefore, the red candidate '8' in cell A7 can be removed since it can 'see' the candidates of both colors.