Menu
Skip Navigation Links.

Sudoku Algorithms

Unique Rectangles (Type 1)
The Unique Rectangles technique assumes that a Sudoku puzzle has only one solution. Any configuration that could lead to multiple solutions is considered invalid. The following image illustrates an example of Unique Rectangles Type 4.
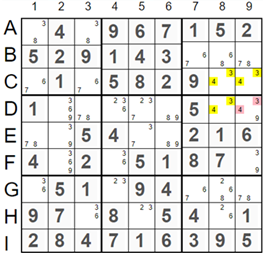
UniqueRectangles Tipe 1 Example The picture on the left shows the Unique Rectangles Type 1 example. Four cells C8, C9, D8, and D9 form a rectangle and have candidates '3' and '4' marked yellow. Cell D9 has an additional possible value, 9. If we remove this candidate, the Sudoku puzzle would have two solutions, as we could alternate values 3 and 4 in cells C8, C9, D8, and D9 without breaking the puzzle. Since a valid Sudoku puzzle can have only one solution, we should remove candidates '3' and '4' (marked red) from cell D9 and assign the value 9 to that cell.

Unique Rectangles (Type 2)
The Unique Rectangles Type 2 Sudoku solving pattern is similar to Type 1. There is a rectangle formed by four cells that have pairs of the same hints in all four of them. While Unique Rectangles Type 1 has one additional hint in one of the four cells, Type 2 has the same additional hint in two of the four cells. The following picture presents an example of the Unique Rectangles Type 2 Sudoku pattern.
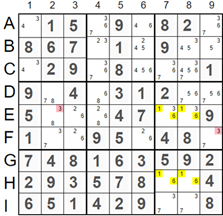
UniqueRectangles Tipe 2 Example Four cells, E7, E8, H7, and H8, form a rectangle and have the same two candidates: '1' and '6' marked yellow. Additionally, cells E7 and E8 have a value of 3 as a candidate. Unlike Type 1, we cannot assign the value 3 to one of the cells since we don’t know whether E7 or E8 should have this value, but we know that the value 3 should be in one of them. This allows us to remove hint 3 from all related cells. Therefore, we can remove hint '3', marked in red from cell F9 since it is in the same square, as well as hint '3', marked in red from cell E2 since it is in the same row as cells E7 and E8.

Unique Rectangles (Type 4)
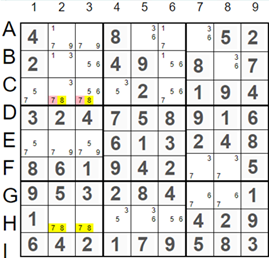
UniqueRectangles Tipe 4 Example Four cells, C2, C3, H2, and H3, form a rectangle. They all have possible values of 7 and 8. These cells may cause multiple puzzle solutions if 7 and 8 remain the only possible values in all four cells. To ensure the uniqueness of the Sudoku solution, we need to exclude at least one of these values from one of the squares. In the lower-left square, hints 7 and 8 are the only possible candidates in cells H2 and H3. The only candidate that can be removed is the value '7', marked in red in cells C2 and C3 since the value 8 is not present in any cell outside of this rectangle. The hint 7 exists outside of cells C2 and C3, so it can be removed from them.
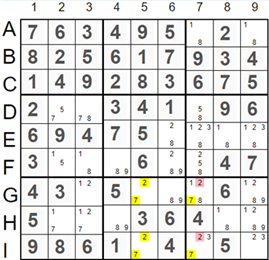
UniqueRectangles Tipe 4 Example The picture on the left presents another example of Unique Rectangles Type 4. Hints 2 and 7 are located in cells G5, G7, I5, and I7, forming a rectangle. These hints will cause multiple Sudoku solutions if we cannot remove one of them from cells G5 and I5, or cells G7 and I7. The hints 2 in cells G7 and I7 are the only candidates that can be removed without breaking the Sudoku rules. To avoid multiple solutions, we should remove hint '2', marked in red, from cells G7 and I7.