Menu
Skip Navigation Links.

Singles Chains Parallel Elimination
The Medusa 3D Parallel Elimination Sudoku solving technique is similar to the Medusa 3D Elimination technique. The difference between these two techniques lies in the first step. For the Medusa 3D Elimination, the first step is to identify a 3x3 square where all cells with a certain candidate are located in one row and one column within the square. For the Medusa 3D Parallel Elimination, the first step is to identify a 3x3 square where all cells with a certain candidate are located in two rows or two columns.

Next, we need to find two cells outside of this square with the same candidate in the selected two rows or columns that are elements of a Medusa 3D chain with the same color. If both outside candidates are ON, all candidates inside the 3x3 square will be eliminated. This scenario is invalid. To avoid the elimination of all inside candidates, we need to remove both outside candidates of the chain as well as all other chain candidates with the same color. All chain candidates with a different color are valid Sudoku solutions.

Following is an example of the Medusa 3D Parallel Elimination technique.

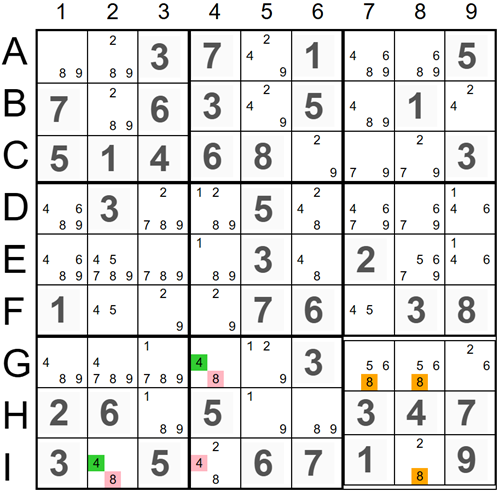
Medusa 3D Parallel Elimination Example The 3x3 square in the bottom right corner has three candidates '8' (marked orange) located in rows G and I. A Medusa 3D chain has five elements marked red and green. One of the red candidates '8' in the Medusa 3D chain is located in row G (G4), and another is in row I (I2) outside of the selected 3x3 square. If the red candidates are ON, all '8' candidates in the selected 3x3 square will be eliminated, making the Sudoku invalid. Therefore, we can remove all Medusa 3D red candidates. The green candidates '4' are valid values and can be assigned to cells I2 and G4.

The X-Chain Details:
  • G4(8) => G4(4) - If 8 in cell G4 is ON, then 4 in cell G4 is OFF.
  • G4(4) => I4(4) - If 4 in cell G4 is OFF, then 4 in cell I4 is ON.
  • I4(4) => I2(4) - If 4 in cell I4 is ON, then 4 in cell I2 is OFF.
  • I2(4) => I2(8) - If 4 in cell I2 is OFF, then 8 in cell I2 is ON.
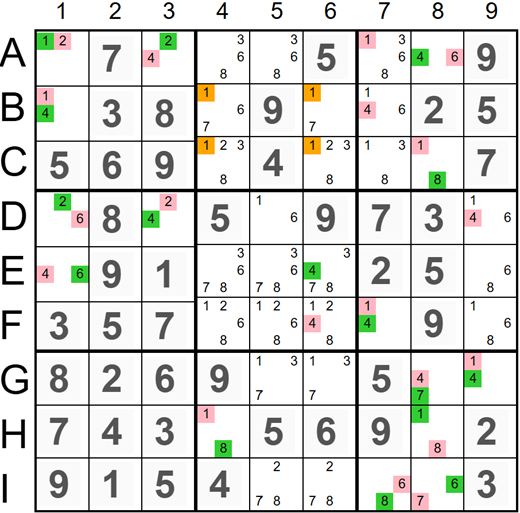
Medusa 3D Parallel Elimination Example An image on the left shows another example of the Medusa 3D Parallel Elimination technique. A 3x3 square in the middle of the top row has four candidates '1' (marked orange) located in rows B and C. The Medusa 3D chain has nineteen red and sixteen green elements. Two of them are located in rows B and C outside of the selected square: candidate '1' in cell B1 and '1' in cell C8. Both candidates are red, and if the red candidates of the Medusa 3D chain are ON, all '1' candidates in the selected 3x3 square will be eliminated. To avoid this scenario, we should remove all red candidates of the Medusa 3D chain. All green candidates are valid, and their values can be assigned to the cells.

The X-Chain Details:
  • B1(1) => A1(1) - If 1 in cell B1 is ON, then 1 in cell A1 is OFF.
  • A1(1) => A7(1) - If 1 in cell A1 is OFF, then 1 in cell A7 is ON.
  • A1(1) => A1(2) - If 1 in cell A1 is OFF, then 2 in cell A1 is ON.
  • A1(2) => D1(2) - If 2 in cell A1 is ON, then 2 in cell D1 is OFF.
  • D1(2) => D3(2) - If 2 in cell D1 is OFF, then 2 in cell D3 is ON.
  • D3(2) => A3(2) - If 2 in cell D3 is ON, then 2 in cell A3 is OFF.
  • A3(2) => A3(4) - If 2 in cell A3 is OFF, then 4 in cell A3 is ON.
  • A3(4) => D3(4) - If 4 in cell A3 is ON, then 4 in cell D3 is OFF.
  • D3(4) => D9(4) - If 4 in cell D3 is OFF, then 4 in cell D9 is ON.
  • D9(4) => G9(4) - If 4 in cell D9 is ON, then 4 in cell G9 is OFF.
  • G9(4) => G8(4) - If 4 in cell G9 is OFF, then 4 in cell G8 is ON.
  • G8(4) => A8(4) - If 4 in cell G8 is ON, then 4 in cell A8 is OFF.
  • A8(4) => B7(4) - If 4 in cell A8 is OFF, then 4 in cell B7 is ON.
  • B7(4) => F7(4) - If 4 in cell B7 is ON, then 4 in cell F7 is OFF.
  • F7(4) => F6(4) - If 4 in cell F7 is OFF, then 4 in cell F6 is ON.
  • F6(4) => E6(4) - If 4 in cell F6 is ON, then 4 in cell E6 is OFF.
  • F7(4) => F7(1) - If 4 in cell F7 is OFF, then 1 in cell F7 is ON.
  • B7(4) => B1(4) - If 4 in cell B7 is ON, then 4 in cell B1 is OFF.
  • B1(4) => E1(4) - If 4 in cell B1 is OFF, then 4 in cell E1 is ON.
  • E1(4) => E1(6) - If 4 in cell E1 is ON, then 6 in cell E1 is OFF.
  • E1(6) => D1(6) - If 6 in cell E1 is OFF, then 6 in cell D1 is ON.
  • A8(4) => A8(6) - If 4 in cell A8 is OFF, then 6 in cell A8 is ON.
  • A8(6) => I8(6) - If 6 in cell A8 is ON, then 6 in cell I8 is OFF.
  • I8(6) => I7(6) - If 6 in cell I8 is OFF, then 6 in cell I7 is ON.
  • I7(6) => I7(8) - If 6 in cell I7 is ON, then 8 in cell I7 is OFF.
  • I7(8) => H8(8) - If 8 in cell I7 is OFF, then 8 in cell H8 is ON.
  • H8(8) => C8(8) - If 8 in cell H8 is ON, then 8 in cell C8 is OFF.
  • C8(8) => C8(1) - If 8 in cell C8 is OFF, then 1 in cell C8 is ON.
  • H8(8) => H4(8) - If 8 in cell H8 is ON, then 8 in cell H4 is OFF.
  • H8(8) => H8(1) - If 8 in cell H8 is ON, then 1 in cell H8 is OFF.
  • H8(1) => H4(1) - If 1 in cell H8 is OFF, then 1 in cell H4 is ON.
  • H8(1) => G9(1) - If 1 in cell H8 is OFF, then 1 in cell G9 is ON.
  • I8(6) => I8(7) - If 6 in cell I8 is OFF, then 7 in cell I8 is ON.
  • I8(7) => G8(7) - If 7 in cell I8 is ON, then 7 in cell G8 is OFF.