Menu
Skip Navigation Links.

X-Chains Elimination
The X-Chains Elimination sudoku solving technique extends the Rectangle Elimination technique by combining it with the X-Chains technique. The Rectangle Elimination technique involves the following steps:

  • Identify a 3x3 square where all cells with a certain candidate are located in one row and one column within the square.
  • Find two cells outside of this square with the same candidate, one in the same row and one in the same column.
  • If there is a scenario where both of these outside candidates can be ON, all candidates inside the 3x3 square will be eliminated. This scenario is invalid, and we should remove the outside candidates that caused this scenario.

According to the X-Chains Elimination technique, the two outside candidates should belong to an X-Chain and have the same color. To avoid the elimination of all inside candidates, we need to remove one outside candidate that belongs to the X-Chain, is located in the same row or column as the inside candidates, and has a weak link to the next element of the chain. This approach is similar to the Rectangle Elimination technique, which involves one strong and one weak link.
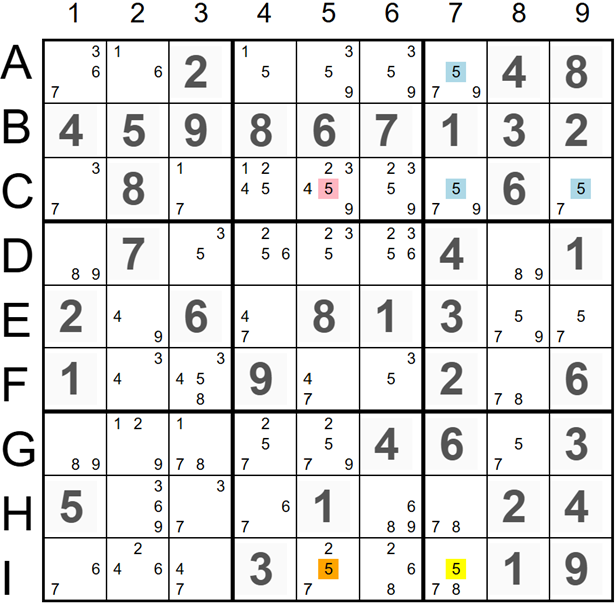
X-Chains Elimination Example An image on the left shows the Rectangle Elimination example with one strong link between candidates '5' in cells I7 and I5, and one weak link between '5' in I5 and C5. If the candidate '5' marked in red in cell C5 is ON, the candidate '5' marked in orange in I5 is OFF, and the candidate '5' marked in yellow in I7 is ON. Candidates '5' in C5 and I7 will eliminate all '5' candidates in the top right 3x3 square and invalidate the sudoku. Therefore, we should remove the candidate '5' marked in red in cell C5. The candidates '5' in cells I7, I5, and C5 present an X-Chain with three candidates. All Rectangle Elimination examples with one strong and one weak link utilize an X-Chain with three candidates, and we can apply the same strategy to any X-Chain that eliminates all candidates in one 3x3 square.
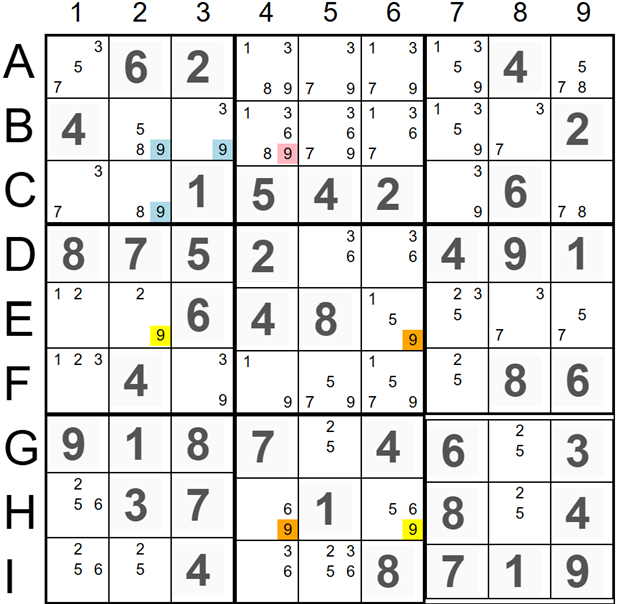
X-Chains Elimination Example Following is an example of the X-Chains Elimination technique that uses an X-Chain with five candidates '9' marked in red, orange, and yellow in cells B4, H4, H6, E6, and E2. The X-Chain details are shown below. If the candidate '9' marked in red in cell B4 is ON, all yellow candidates '9' are ON. In this case, candidates '9' in B4 and E2 would eliminate all candidates '9' (marked in blue) in the top left 3x3 square, making the sudoku invalid. Therefore, we should remove the candidate '9' marked in red in cell B4.
The X-Chain Details:
  • B4(9) => H4(9) - Weak Link: If 9 in cell B4 is ON, then 9 in cell H4 is OFF.
  • H4(9) -> H6(9) - Strong Link: If 9 in cell H4 is OFF, then 9 in cell H6 is ON.
  • H6(9) => E6(9) - Weak Link: If 9 in cell H6 is ON, then 9 in cell E6 is OFF.
  • E6(9) -> E2(9) - Strong Link: If 9 in cell E6 is OFF, then 9 in cell E2 is ON.
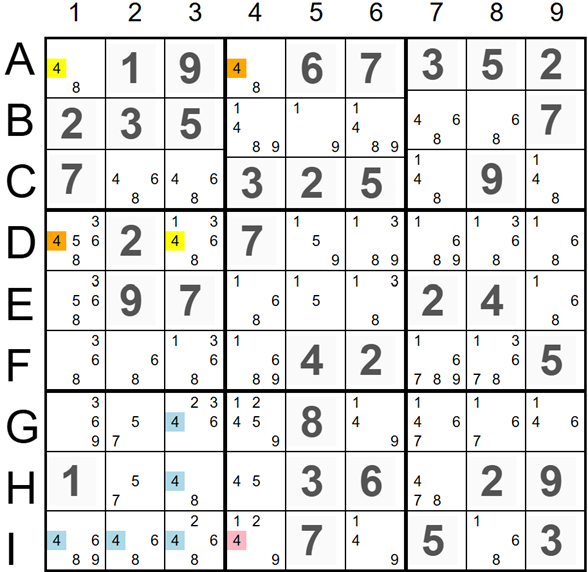
X-Chains Elimination Example The image on the left illustrates another example of the X-Chains Elimination technique. The bottom-left 3x3 square contains five cells with the candidate '4' marked in blue. All of these cells are located in row I and column 3. Any chain with a candidate '4' in row I and column 3 outside of this square will invalidate the puzzle. The X-Chain, highlighted in red, orange, and yellow, has five candidates '4'. If the candidate '4' marked in red in cell I4 is ON, the candidate '4' marked in orange in cells A4 and D1 will be OFF, and the candidates marked in yellow in cells A1 and D3 will be ON. In this case, all candidates '4' in the bottom-left 3x3 square will be eliminated. To avoid the elimination of the candidate '4', we should remove the candidate '4' marked in red in cell I4.
The X-Chain Details:
  • I4(4) => A4(4) - Weak Link: If 4 in cell I4 is ON, then 4 in cell A4 is OFF.
  • A4(4) -> A1(4) - Strong Link: If 4 in cell A4 is OFF, then 4 in cell A1 is ON.
  • A1(4) => D1(4) - Weak Link: If 4 in cell A1 is ON, then 4 in cell D1 is OFF.
  • D1(4) -> D3(4) - Strong Link: If 4 in cell D1 is OFF, then 4 in cell D3 is ON.