Menu
Skip Navigation Links.

Singles Chains Elimination
The Singles Chains Elimination sudoku solving technique extends the Rectangle Elimination technique by combining it with the Singles Chains technique. The Rectangle Elimination technique involves the following steps:

  • Identify a 3x3 square where all cells with a certain candidate are located in one row and one column within the square.
  • Find two cells outside of this square with the same candidate, one in the same row and one in the same column.
  • If there is a scenario where both of these outside candidates can be ON, all candidates inside the 3x3 square will be eliminated. This scenario is invalid, and we should remove the outside candidates that caused this scenario.

With the Singles Chains Elimination technique, the two outside candidates should belong to a Single Chain and have the same color. To avoid the elimination of all inside candidates, we need to remove both outside candidates of the chain that are located in the same row and one in the same column, as well as all other chain candidates with the same color. All chain candidates with a different color are valid Sudoku solutions. This approach is similar to the Rectangle Elimination technique with two strong links.
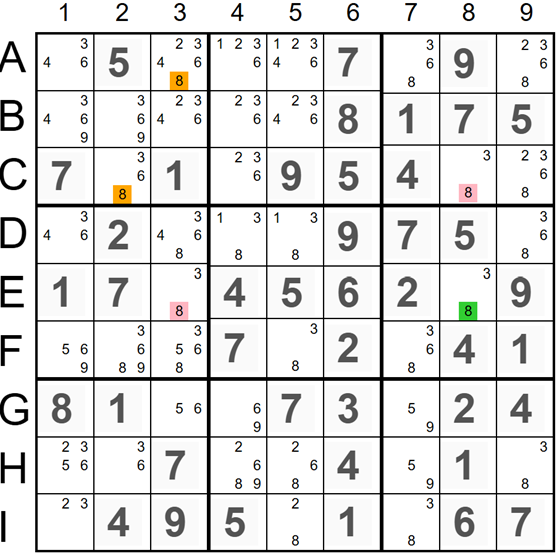
Singles Chains Elimination Example An image on the left shows the Rectangle Elimination example with two strong links. The links between candidate '8' in E2, E8, and C8 are strong. This means that if one red candidate is ON, all red candidates should be ON, and all green candidates should be OFF. If the red candidates '8' in E2 and C8 are ON, all orange '8' candidates in the top left 3x3 square would be eliminated, invalidating the puzzle. Therefore, we can remove the red candidates in E2 and C8. In this example, the three '8' candidates in E2, E8, and C8 form a Singles Chain, as they are connected by strong links. The Rectangle Elimination technique with two strong links always utilizes a single chain with three candidates. The Singles Chains Elimination technique extends this approach by utilizing more complex Singles Chains.
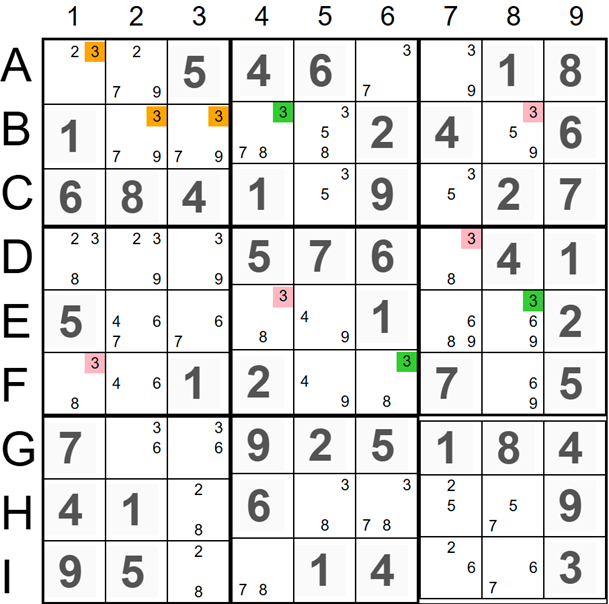
Singles Chains Elimination Example The next example shows a Singles Chains Elimination technique that presents a single chain with seven candidates. If the red candidate '3' in cell F1 is ON, all red candidates (in cells E4, D7, and B8) should be ON, and all green candidates (in cells F6, E8, and B4) should be OFF. In this scenario, all candidates '3' marked orange in the top left 3x3 square would be eliminated, making the sudoku invalid. Therefore, we should remove all candidates '3' marked red.
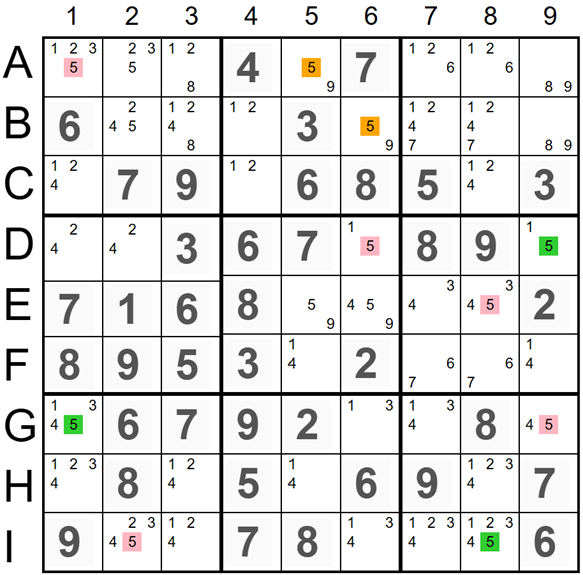
Singles Chains Elimination Example An image on the left shows another example of the Singles Chains Elimination technique. The Singles Chain includes five red candidates '5' (in cells A1, D6, E8, G9, and I2), and three green candidates '5' (in cells D9, G1, and I8). Orange candidates '5' in the top middle 3x3 square will be eliminated if the Singles Chain red candidates are ON. Therefore, we can remove all red candidates and assign the value '5' to all cells with green candidates.