Menu
Skip Navigation Links.

Singles Chains Parallel Elimination
The Singles Chains Parallel Elimination sudoku solving technique is similar to the Singles Chains Elimination technique.

The first step of the Singles Chains Elimination technique requires identifying a 3x3 square where all cells with a certain candidate are located in one row and one column within the square. In contrast, for the Singles Chains Parallel Elimination, we need to find a 3x3 square where all cells with a certain candidate are located in two rows or two columns within the 3x3 square.

If there is a Single Chain with candidates in those two rows or two columns (outside of the 3x3 square) with the same color, all candidates with the same color can be removed. Otherwise, all selected candidates in the 3x3 square would be eliminated, making the sudoku invalid. All chain candidates with a different color are valid sudoku solutions.

In the following example, the middle 3x3 square in the first row has two candidates '1' (marked orange) located in rows B and C.

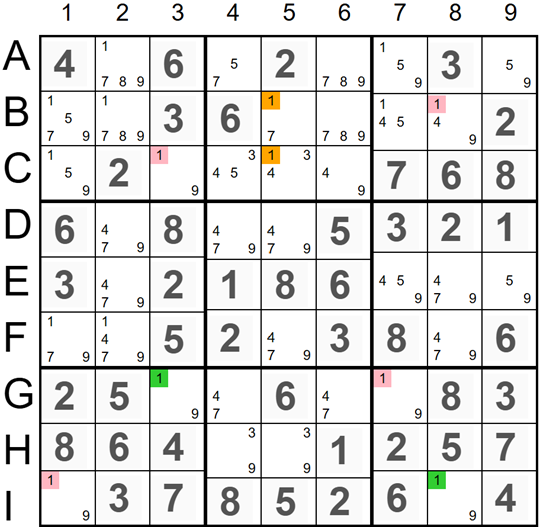
Singles Chains Parallel Elimination Example A Singles Chain has six candidates: four red candidates '1' in cells C3, B8, G7, and I1, and two green candidates in G3 and I8. If the red candidates '1' in C3 and B8 are ON, all other candidates '1' in rows B and C should be eliminated, including both candidates '1' (marked orange) in the middle 3x3 square in the first row. This would make the sudoku invalid. To avoid this scenario, all Singles Chain red candidates should be OFF. All green candidates should be assigned to the cells as valid sudoku solutions.

The X-Chain Details:
  • B8(1) => I8(1) - If 1 in cell B8 is ON, then 1 in cell I8 is OFF.
  • I8(1) => I1(1) - If 1 in cell I8 is OFF, then 1 in cell I1 is ON.
  • I1(1) => G3(1) - If 1 in cell I1 is ON, then 1 in cell G3 is OFF.
  • G3(1) => C3(1) - If 1 in cell G3 is OFF, then 1 in cell C3 is ON.
  • I8(1) => G7(1) - If 1 in cell I8 is OFF, then 1 in cell G7 is ON.
Singles Chains Parallel Elimination Example The next example of the Singles Chains Parallel Elimination is presented in the image on the left. Three candidates '4' are marked orange in the top left 3x3 square located in columns 1 and 3. A Singles Chain has six candidates '4' marked red and green. Two red chain elements are located in columns 1 and 4 as well. If those two candidates are ON, all candidates '4' in the top left 3x3 square should be eliminated, and the sudoku would be invalidated. To avoid this scenario, we should remove all red candidates. The value of the green candidates is a valid sudoku solution and should be assigned to the cells F8 and H9.

The X-Chain Details:
  • H1(4) => H9(4) - If 4 in cell H1 is ON, then 4 in cell H9 is OFF.
  • H9(4) => D9(4) - If 4 in cell H9 is OFF, then 4 in cell D9 is ON.
  • D9(4) => F8(4) - If 4 in cell D9 is ON, then 4 in cell F8 is OFF.
  • F8(4) => G8(4) - If 4 in cell F8 is OFF, then 4 in cell G8 is ON.
  • F8(4) => F3(4) - If 4 in cell F8 is OFF, then 4 in cell F3 is ON.