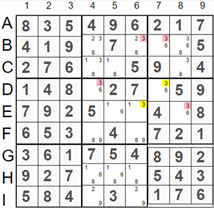
There are two sets of single candidates for the number 3: E6 and D7, marked in yellow, and B5, B7, D4, and E8, marked in red. The two red candidates in cells B6 and B7 are in the same row, which contradicts the sudoku rule. Therefore, all candidates marked in red in cells B5, B7, D4, and E8 can be removed, and the value
'3' can be assigned to the cells E6 and D7, marked in yellow.