Menu
Skip Navigation Links.

X-Chains Parallel Elimination
The X-Chains Parallel Elimination Sudoku solving technique is similar to the X-Chains Elimination technique.

For the X-Chains Elimination, we need to identify a 3x3 square where all cells with a certain candidate are located in one row and one column within the 3x3 square. Instead, the X-Chains Parallel Elimination technique works when there is a 3x3 square where all cells with a certain candidate are located in two rows or two columns.

To apply the X-Chains Parallel Elimination technique, we need to find an X-Chain with the same candidates and the same color in cells outside of the square in the selected two rows or columns. One of these candidates should have a weak link. If this candidate is ON, all candidates of the same color should be ON. In this case, all candidates inside the 3x3 square will be eliminated, which makes the Sudoku invalid. To avoid the elimination of all inside candidates, we should remove the candidate with a weak link.
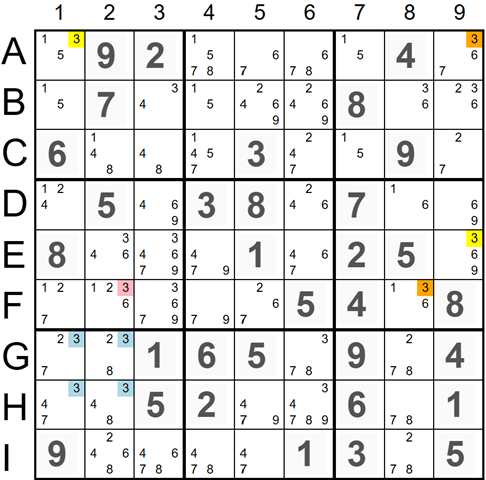
X-Chains Parallel Elimination Example An image on the left shows an example of the X-Chains Parallel Elimination technique. The bottom-left 3x3 square has four '8' candidates (marked in blue) located in rows G and H, specifically in cells G1, G2, H2, and H3. An X-Chain of '8' candidates has five elements. One element is in row G (cell G7), and another is in row H (cell H5). The '8' candidate in cell H5, has a weak link to the next element of the X-Chain, marked in orange in cell B5. If the '8' in cell H5 is ON, all orange elements of the chain are OFF, and all yellow elements are ON. In this scenario, both elements of the X-Chain in rows G (cell G7) and H (cell H5) are ON, and all other '8' candidates in these rows will be eliminated, leaving the bottom-left 3x3 square without any '8' candidates. To avoid this scenario, we should remove the '8' candidate marked in red in cell H5.

The X-Chain Details:
  • H5(8) => B5(8) - Weak Link: If 8 in cell H5 is ON, then 8 in cell B5 is OFF.
  • B5(8) -> B8(8) - Strong Link: If 8 in cell B5 is OFF, then 8 in cell B8 is ON.
  • B8(8) => I8(8) - Weak Link: If 8 in cell B8 is ON, then 8 in cell I8 is OFF.
  • I8(8) -> G7(8) - Strong Link: If 8 in cell I8 is OFF, then 8 in cell G7 is ON.
X-Chains Parallel Elimination Example Another example shows a case where two elements of the X-Chain, '3' marked in yellow in cell A1 and '3' marked in red in cell F2, are located in the same two columns as all four '3' candidates (marked in blue) in the bottom-left 3x3 square. There is a weak link, between the candidate '3' in cell F2 and the candidate '3' (marked in orange) in cell F8. If the candidate '3' in F2 is ON, all orange elements of the X-Chain are OFF, and the yellow elements are ON. In this case, the candidates '3' in column 1 (cell A1) and column 2 (cell F2) are ON, and all candidates '3' (marked in blue) in the bottom-left 3x3 square will be eliminated. This scenario would invalidate the puzzle; therefore, the '3' in cell F2 cannot be ON and should be removed.

The X-Chain Details:
  • F2(3) => F8(3) - Weak Link: If 3 in cell F2 is ON, then 3 in cell F8 is OFF.
  • F8(3) -> E9(3) - Strong Link: If 3 in cell F8 is OFF, then 3 in cell E9 is ON..
  • E9(3) => A9(3) - Weak Link: If 3 in cell E9 is ON, then 3 in cell A9 is OFF.
  • A9(3) -> A1(3) - Strong Link: If 3 in cell A9 is OFF, then 3 in cell A1 is ON.