Menu
Skip Navigation Links.

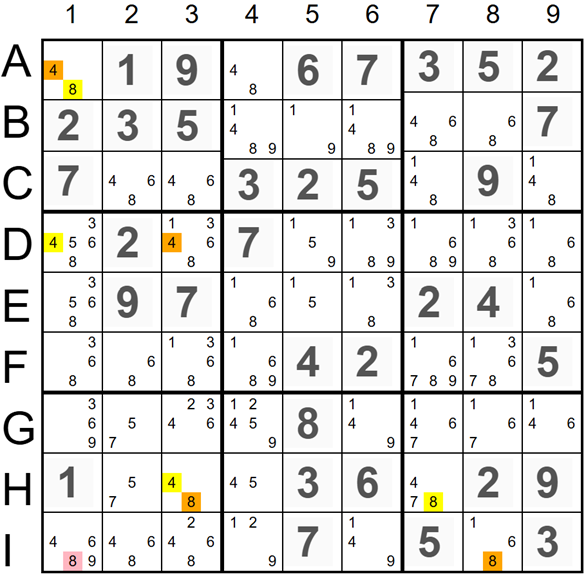
Sudoku Algorithms - XY-Chains

XY-Chains
The XY-Chains technique is an extension of X-Chains. With the X-Chains technique, we link the same candidates in different cells of the same row, column, or 3x3 square. In addition to the X-Chains linking technique, XY-Chains allows us to link different candidates within the same cell. Similar to X-Chains, XY-Chains is a coloring technique that uses alternating strong and weak links. The main advantage of this coloring technique is that if any candidate of one color is a valid solution, then all other candidates of the same color are also solutions, and all candidates of the other color should be removed.

XY-Chains - Two Colours 'Elsewhere'
XY-Chain We start our XY-Chain in cell A1 by coloring candidate '8' yellow. There is a strong link between candidates 8 and 4 in cell A1. If 8 is a valid solution, candidate 4 should be removed, and vice versa. So, we can color candidate '4' orange. Now, we have a weak link between candidate 4 in A1 and D1 since there is another candidate 4 in column 1. We can continue this alternate coloring process until we reach cell I8, making candidate 8 orange. Now, candidate '8' marked red in cell I1 can ‘see’ the yellow candidate '8' in cell A1 and the orange '8' in cell I8. According to the chain rule, either all yellow or all orange candidates are a valid solution. Candidate 8 in cell I1 should be removed since it ‘sees’ a valid candidate 8 in any scenario.
XY-Chain The image on the left shows another example of XY-Chains. The chain includes four different candidates: 2, 3, 5, and 9. Candidate '5', marked red in cell C4, can ‘see’ the yellow candidate '5' in the same row in cell C6 and the orange '5' in the same column in cell H5. According to the chain rules, candidate 5 in cell C4 should be removed.
Sponsored Links